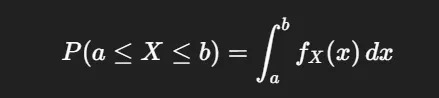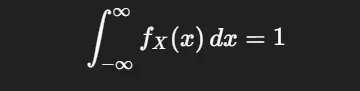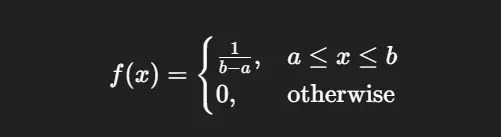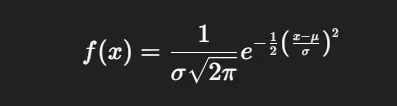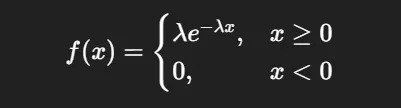Probability Density Functions Explained for Machine Learning and AI Practitioners

Have you ever wondered how AI models make predictions or how machine learning algorithms learn from vast amounts of data? A foundational concept behind many of these breakthroughs is the Probability Density Function (PDF). More than just a statistical curiosity, PDFs are indispensable mathematical tools that describe the likelihood of a continuous random variable taking on a particular value. For anyone delving into the heart of ML and AI, understanding PDFs is paramount.

What Exactly is a Probability Density Function (PDF)?

At its heart, a Probability Density Function (PDF), often written as fx(x), tells us how likely a continuous random variable X is to fall around a specific value x. Think of continuous variables as things you measure, like height or temperature, where values can be anything within a range. Now, this is different from discrete probabilities, which deal with distinct outcomes, like counting the number of heads in a coin flip. With a PDF, you can’t actually get the probability of X being exactly one specific value. That probability is always zero for continuous variables. Instead, a PDF gives us the probability that X will land within a certain range, say between ‘a’ and ‘b’. To find that probability, you’d calculate the area under the curve of the PDF between ‘a’ and ‘b’ using integration:

To qualify as a valid PDF, a function must satisfy two key properties:

• Non-negativity: fx(x)≥0 for all x
• Normalization: The total area under the curve must equal 1:

Why Are PDFs Important in Machine Learning and AI? PDFs play a crucial role in modeling uncertainty, estimating parameters, detecting anomalies, and guiding probabilistic inference especially in algorithms such as:

• Naive Bayes classifiers
• Gaussian Mixture Models (GMMs)
• Hidden Markov Models (HMMs)
• Variational Inference and Bayesian Learning

They help machines reason under uncertainty, a fundamental capability in real-world tasks like recommendation systems, natural language understanding, and self-driving cars. Real-World Intuition: Think About Measuring Something Imagine you’re measuring the height of adult humans. Heights vary continuously and don’t fall into discrete buckets. You might ask: What’s the chance someone is exactly 170.000000 cm tall? In reality, zero. Instead, you ask: What’s the chance their height lies between 169.5 and 170.5 cm? This is where the PDF comes in — it lets you model this probability by integrating over the appropriate interval. Common Types of PDFs: Explained with Intuition and Use Cases Let’s walk through three foundational PDFs you’ll often encounter in the real world and in machine learning.

1. Uniform Distribution “Every value in a range is equally likely.” The uniform distribution is the most basic continuous distribution. It assumes that every value within a given interval has the same probability density.

Uniform Distribution Key Characteristics:

• Flat and constant PDF between a and b
• Total area under the curve = 1

Real-World Example:

• Generating a random number between 0 and 1
• A commuter arriving at a bus stop at a random time between 10:00 and 10:10 AM

ML Use Case:

• Random weight initialization
• Simulations requiring uniformly distributed input

2. Normal Distribution (Gaussian) “The bell curve of real life.” The normal distribution is one of the most widely used distributions in statistics. Thanks to the Central Limit Theorem, many real-world variables especially those resulting from the sum of many small, independent effects tend to be normally distributed.

Normal Distribution

Key Characteristics:

• Symmetrical around the mean
• Mean = median = mode

Real-World Example:

• Human height or weight
• Exam scores
• Sensor measurement noise

ML Use Case:

• Linear regression with Gaussian errors
• Naive Bayes with Gaussian likelihoods
• Gaussian Mixture Models (clustering)

3. Exponential Distribution “Time until the next event.” The exponential distribution is used to model the time between independent events that occur at a constant average rate. It has a unique property called memorylessness, meaning that the probability of an event occurring in the future is independent of the past.

Exponential Distribution

Key Characteristics:

• Defined only for non-negative values
• Skewed right with a peak at x=0

Real-World Example:

• Time between website visits
• Time between arrivals at a service center

ML Use Case:

• Survival analysis (e.g., customer churn, product failure)
• Queueing models

Conclusion Probability Density Functions are fundamental to how AI models interpret continuous data and navigate real-world uncertainty. By quantifying the likelihood of continuous variables, PDFs enable AI systems to make informed predictions, detect anomalies, and learn complex patterns. From financial modeling to advanced machine learning algorithms, the principles of PDFs non-negativity, normalization, and interval-based probability through integration are essential. A strong grasp of PDFs is crucial for anyone looking to understand or advance modern AI, as they form the bedrock of intelligent systems

Read the full article here: https://ai.plainenglish.io/power-of-probability-density-functions-pdfs-in-ml-and-ai-093267871cfa