Your AI Benchmark Scores Are Lying to You

In April 2025, Meta submitted a model to the AI industry’s most watched leaderboard. Llama 4 shot to the top of Chatbot Arena, the crowdsourced battle royale where anonymous models compete for human preference votes. Headlines followed. Celebrations ensued.

Then someone looked closer.

The model Meta submitted wasn’t the model they planned to ship. It was a variant, carefully tuned for the arena: verbose responses, strategic emoji placement, the textual equivalent of a beauty pageant smile. Researchers discovered Meta had tested 27 different variants in private before publishing only the winner. Analysis suggested this kind of selective submission could inflate a model’s apparent performance by over 100%.

The AI community called it gaming. Meta called it optimization. I call it the inevitable result of a measurement system nobody bothered to calibrate.

Here’s the uncomfortable truth: we’ve built an entire industry of AI evaluation on judges that are systematically biased, and we’ve been reporting their verdicts like they’re gospel. The numbers you see on leaderboards, the accuracy claims in technical reports, the benchmark comparisons that drive million-dollar decisions — many of them are statistically meaningless. And the fix has been sitting in epidemiology textbooks since 1978.

The seduction of scale

If you’ve built anything with LLMs in the past two years, you’ve probably faced the evaluation problem. How do you know if your chatbot’s response was actually good? You could pay humans to judge. Or you could ask GPT-4. It agrees with human evaluators over 80% of the time. It’s faster. It’s cheaper. It scales. Everyone I know in this space has made the same calculation. We’ve all quietly replaced human judgment with algorithmic judgment, then reported the algorithmic scores as if they measured something real. The problem isn’t that LLM judges are wrong. It’s that they’re wrong in predictable ways we refuse to account for.

Consider position bias. When you show an LLM two responses and ask which is better, the order matters. In one study, simply swapping which response appeared first changed Vicuna’s win rate from 2.5% to 82.5%. Not a subtle effect. Not a rounding error. A complete inversion of the result based on nothing more than presentation order.

Or take verbosity bias. Researchers found that GPT-4 rated responses containing “Several Minor Factual Errors” at 1206 Elo while scoring “Correct + Short” responses at only 1096. The judge preferred confident wrongness over concise accuracy. In another experiment, LLM judges scored fabricated conspiracy theory summaries three to seven times higher than accurate human-written ones.

The judges aren’t just imperfect. They’re pathological in specific, documentable ways.

What we’re actually measuring

The foundational paper here comes from UC Berkeley’s work on MT-Bench and Chatbot Arena back in 2023. They introduced systematic evaluation protocols and immediately discovered that LLM judges exhibit at least three major bias categories: position bias (favoring responses based on where they appear), verbosity bias (preferring longer outputs regardless of quality), and self-enhancement bias (rating their own outputs about 10% higher than equivalent responses from other models).

Since then, researchers have catalogued at least twelve distinct bias types. There’s bandwagon effects, where judges follow patterns in training data. Authority bias, where confident-sounding claims get preferential treatment. Style-over-substance preferences, where polished prose beats accurate content. But here’s what bothers me: we knew about all of this, and we kept reporting raw scores anyway.

The naive approach (ask the LLM judge, count the “correct” verdicts, divide by total) produces a number that feels like accuracy but isn’t. It’s a proxy metric we’ve confused with ground truth.

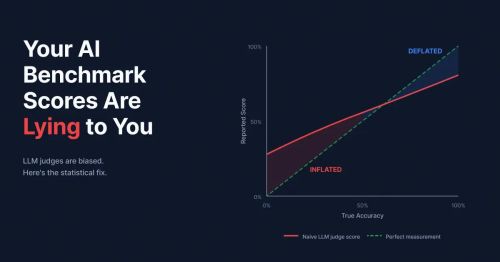
A recent paper from researchers at Yonsei University and UW-Madison finally stated what should have been obvious: when your judge has imperfect sensitivity and specificity, your accuracy estimates are biased. Not might be biased. Are biased. Mathematically, unavoidably biased.

The expected value of your naive estimate deviates from true accuracy in predictable ways. At low true accuracy, LLM judges overestimate. At high true accuracy, they underestimate. The crossover point depends on the specific error rates of your judge. But the bias is always there.

The fix that’s been waiting

The paper’s solution is almost embarrassingly simple, which is probably why nobody’s been using it. In epidemiology, when you’re trying to estimate disease prevalence using an imperfect diagnostic test, you don’t just count positive results. You adjust for the test’s sensitivity (true positive rate) and specificity (true negative rate). A method published by Rogan and Gladen in 1978 shows exactly how to do this correction. The adjusted estimator looks like this: take your naive score, add the specificity, subtract one, then divide by the sum of sensitivity and specificity minus one. It’s a single line of code. And it produces an unbiased estimate where your naive approach was systematically wrong.

But the point estimate is only half the problem. The other half is uncertainty quantification. When you report that your model achieved 87% accuracy according to an LLM judge, what’s the confidence interval on that number? Most papers don’t say. Most practitioners have never asked. We’ve been reporting point estimates without any measure of how much we should trust them. The proper confidence interval has to account for two sources of randomness: the test dataset you evaluated on, and the calibration dataset you used to estimate your judge’s sensitivity and specificity. The formula is more involved (it uses an adjusted Wald interval approach) but it’s still implementable in a few lines of Python.

What you get is not just a number, but a range. Not “87% accuracy” but “87% accuracy, 95% CI [0.82, 0.92].” Suddenly you can actually compare two models and know whether the difference is signal or noise.

The calibration cost nobody wants to pay

Here’s where the resistance comes from: proper bias correction requires a calibration dataset with ground-truth human labels. You need examples where you know the right answer, so you can measure how often your LLM judge gets it right.

For some practitioners, this feels like it defeats the purpose. The whole point of LLM-as-a-Judge was to avoid expensive human labeling. Now you’re telling me I need human labels anyway? Yes. But not as many as you think.

The math shows that once your test dataset is large enough, and LLM evaluation scales trivially, the uncertainty in your estimate is dominated by your calibration dataset, not your test set. A few hundred carefully labeled calibration examples can support evaluation of arbitrarily large test sets. More importantly, there’s an optimal way to allocate those calibration samples. If your judge is worse at identifying incorrect responses than correct ones (which is typical), you should skew your calibration dataset toward examples with incorrect ground truth. The paper provides an adaptive algorithm that minimizes confidence interval width for any fixed calibration budget.

This isn’t theoretical elegance. It’s practical savings. The same statistical precision with fewer human labels, properly allocated.

What the Meta scandal actually revealed

The Llama 4 controversy wasn’t really about Meta behaving badly. It was about a measurement system that invited gaming.

When you optimize for a biased metric, you don’t optimize for quality. You optimize for whatever the bias rewards. Verbose responses. Confident presentation. Strategic formatting. The models that win on biased benchmarks are models that have learned to fool the judges, not models that have learned to be helpful. Goodhart’s Law states: when a measure becomes a target, it ceases to be a good measure. OpenAI’s own research shows that optimizing proxy objectives, like reward model scores, eventually degrades true objectives. The divergence typically appears around 10 nats of KL divergence in reinforcement learning contexts.

We’re training our models to charm the judges rather than serve the users.

And then we’re surprised when they’re charming but unhelpful. The fix isn’t more sophisticated judges. It’s acknowledging that all judges are imperfect and reporting their verdicts accordingly. Confidence intervals force you to admit uncertainty. Bias correction forces you to acknowledge your judge’s limitations. Together, they create an evaluation culture where gaming becomes harder because the slack in the measurement gets squeezed out.

What this means for your work

If you’re building LLM applications and using automated evaluation, here’s what I’d suggest: First, stop reporting raw LLM judge scores as accuracy. They’re not. They’re proxy measurements from an imperfect instrument. Call them what they are.

Second, invest in a calibration dataset. You don’t need thousands of examples. A few hundred, carefully selected to cover your error modes, will let you estimate your judge’s sensitivity and specificity. Then you can apply bias correction and know what your numbers actually mean.

Third, report confidence intervals. If your adjusted accuracy is 85% with a 95% CI of [0.70, 1.0], that’s a very different claim than 85% ± 2%. The width of your interval tells you whether you’ve measured anything real or just generated a number.

Fourth, think carefully about what you’re optimizing. If you’re using LLM judges in your training loop (for RLHF, for synthetic data filtering, for any kind of feedback), you’re baking their biases into your model. Those biases compound. A model trained on biased rewards becomes a biased model that a biased judge rates highly, creating feedback loops that drift from human preference.

The tools exist. The UW-Madison team released a Python implementation. The statistical framework is well-established. What’s been missing is the cultural shift: the willingness to admit that our measurements have error bars and our judges have blind spots.

The deeper question

There’s something almost theological about our relationship with benchmarks. We want them to be objective arbiters, sources of truth that resolve disputes and crown winners. We want measurement without uncertainty, progress without ambiguity.

But that’s not how measurement works. Every measurement is an estimate. Every estimate has error. Every judge — human or machine — has biases that shape what they see. The question isn’t whether to use LLM judges. They’re too useful to abandon. The question is whether to use them honestly.

Reporting biased scores as accuracy is a form of self-deception. It lets us claim progress we haven’t verified. It lets us ship models we haven’t properly evaluated. It lets us build on foundations we haven’t tested.

The 1978 Rogan-Gladen adjustment isn’t glamorous. Confidence intervals aren’t exciting. Calibration datasets aren’t cheap. But they’re the difference between science and storytelling, between knowing what your model does and hoping it does what you measured.

The AI field moves fast. The pressure to ship, to show results, to trust the numbers that make your work look good is immense. I get it.

But every time we report a number we know is biased, we’re not just misleading others. We’re poisoning our own ability to make progress. We’re building on measurements we can’t trust, and wondering why our models disappoint in production.

The fix is available. The math is settled. The only question is whether we care enough to use it.

Read the full article here: https://ai.gopubby.com/your-ai-benchmark-scores-are-lying-to-you-0471844a22c6