How I Learned Monads: Not Through Haskell But Through Rust
I approached learning monads in Haskell wrong and failed. Then I discovered I’d been using them in Rust all along without knowing.
Introduction About a decade ago, I tried to learn Haskell. I was mesmerized by its elegance — the way types guided you toward correct programs, how pure functions composed so naturally, the terseness that still remained readable. I worked through A Gentle Introduction to Haskell, and everything made sense until I hit the chapter of monads. The book presented monads like this: class Monad m where
return :: a -> m a (>>=) :: m a -> (a -> m b) -> m b (>>) :: m a -> m b -> m b fail :: String -> m a
Then it stated the monad laws: -- left identity return a >>= f ≡ f a -- right identity m >>= return ≡ m -- associativity (m >>= f) >>= g ≡ m >>= (\x -> f x >>= g) And gave examples with the list monad: -- list monad instance instance Monad [] where
return x = [x] xs >>= f = concat (map f xs)
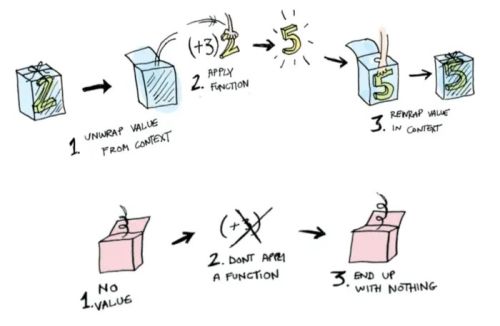
-- example usage [1,2,3] >>= \x -> [x, -x] -- [1,-1,2,-2,3,-3] I stared at this for hours. What was >>= supposed to mean? Why did we need these specific laws? The list example worked, but I couldn't see why this pattern was useful or how I'd recognize when to use it. The IO monad was even more mysterious -- it seemed like special compiler magic rather than a pattern I could understand. I eventually moved on, thinking monads were just one of those things you needed a PhD to truly grasp. I could use do notation when I had to, but I never felt like I understood what was happening underneath. Fast forwarding to 2024–2025, while I was writing some Rust codes, something clicked. I realized I’d been using monads all along. Every time I chained .map() calls on an Option<T> or used the ? operator with Result<T, E>, I was working with monadic patterns. The difference was that Rust let me build up to the abstraction from concrete code I was already writing. I didn't start with type classes and laws -- I started with solving real problems and noticed the patterns emerging. This is the story of how I learned to see the patterns that were already in my code.
Starting With What I Already Knew Here’s some Rust code I wrote early on, before I understood what monads were: fn divide(a: i32, b: i32) -> Option<i32> {
if b == 0 {
None
} else {
Some(a / b)
}
}
fn main() {
let result = divide(10, 2)
.map(|x| x * 2)
.map(|x| x + 1);
println!("{:?}", result); // Some(11)
} This felt completely natural to me. It’s just Rust being Rust. But later I learned this innocent-looking code was demonstrating several sophisticated mathematical concepts. Let me show you how I unpacked them.
First A-Ha: The Monoid Hiding in Plain Sight I started noticing a pattern when I tried to combine Option values. My first attempt was clunky: fn combine_strings(a: Option<String>, b: Option<String>) -> Option<String> {
match (a, b) {
(Some(x), Some(y)) => Some(x + &y),
_ => None,
}
}
fn main() {
let hello = Some("Hello, ".to_string());
let world = Some("World!".to_string());
let empty: Option<String> = None;
println!("{:?}", combine_strings(hello.clone(), world.clone())); // Some("Hello, World!")
println!("{:?}", combine_strings(hello.clone(), empty.clone())); // None
} But this bothered me. Why should combining with None always give us None? What if I wanted to preserve the successful values? I tried a different approach: impl<T> Option<T> where
T: Clone + std::ops::Add<Output = T>
{
fn combine(self, other: Option<T>) -> Option<T> {
match (self, other) {
(Some(a), Some(b)) => Some(a + b),
(Some(a), None) => Some(a),
(None, Some(b)) => Some(b),
(None, None) => None,
}
}
}
fn main() {
let a = Some("Hello".to_string());
let b = Some(" World".to_string());
let result = a.clone().combine(b.clone());
println!("{:?}", result); // Some("Hello World")
// wait, this is interesting...
let with_empty = a.clone().combine(Some(String::new()));
println!("{:?}", with_empty); // Some("Hello")
// and the order doesn't matter!
let left = a.clone().combine(b.clone()).combine(Some("!".to_string()));
let right = a.clone().combine(b.clone().combine(Some("!".to_string())));
println!("{:?} == {:?}", left, right); // both Some("Hello World!")
} That’s when it hit me — I’d stumbled onto a monoid. I remembered from my college abstract algebra class that a monoid is just:
- An associative operation: (a⊕b)⊕c=a⊕(b⊕c)
- An identity element: ∃e such that a⊕e=e⊕a=a
In my case, the operation was combine, and the identity was Some(String::new()). The fact that I could combine multiple Option values without worrying about the order felt powerful. This was my first glimpse that the patterns in my Rust code had deeper mathematical structure.
Second A-Ha: I’d Been Using Functors All Along I started looking more carefully at that .map() operation I'd been using everywhere: fn main() {
let number = Some(5);
let doubled = number.map(|x| x * 2);
let stringified = doubled.map(|x| x.to_string());
println!("{:?}", stringified); // Some("10")
// this chaining felt so natural, but why did it work so well?
let result = Some(5)
.map(|x| x * 2)
.map(|x| x.to_string())
.map(|s| format!("Result: {}", s));
println!("{:?}", result); // Some("Result: 10")
} I started experimenting. What if I mapped with the identity function? What about composing functions? fn identity<T>(x: T) -> T { x } fn add_one(x: i32) -> i32 { x + 1 } fn double(x: i32) -> i32 { x * 2 } fn main() {
let value = Some(5);
// mapping with identity does nothing
let mapped_identity = value.map(identity);
println!("{:?} == {:?}", value, mapped_identity); // Some(5) == Some(5)
// and composition works exactly as I'd expect
let composed_separate = value.map(add_one).map(double);
let composed_together = value.map(|x| double(add_one(x)));
println!("{:?} == {:?}", composed_separate, composed_together); // Some(12) == Some(12)
} This revealed that Option<T> is a functor. A functor preserves:
- Identity: map(id)=idmap(id)=id
- Composition: map(f)∘map(g)=map(g∘f)map(f)∘map(g)=map(g∘f)
The functor pattern meant I could transform values inside a context (like Option, Result, Vec) without manually unwrapping and rewrapping. That's why the chaining felt so natural. But there was more to discover. Option<T> is specifically an endofunctor -- it maps from Rust types to Rust types. It takes a T and gives you back an Option<T>, staying within the same type system. This detail would become important later.
Third A-Ha: When One Argument Isn’t Enough Then I ran into a problem. What if I wanted to apply a function that takes multiple arguments? fn add(a: i32, b: i32) -> i32 {
a + b
}
fn main() {
let a = Some(5);
let b = Some(3);
// this doesn't work with map:
// let result = a.map(|x| add(x, ???)); // what goes here?
// I fell back to pattern matching
let result = match (a, b) {
(Some(x), Some(y)) => Some(add(x, y)),
_ => None,
};
println!("{:?}", result); // Some(8)
} This pattern showed up so often that I tried to abstract it. I created an applicative functor interface: trait Apply<T> {
fn apply<U, F>(self, f: Option<F>) -> Option where F: FnOnce(T) -> U;
}
impl<T> Apply<T> for Option<T> {
fn apply<U, F>(self, f: Option<F>) -> Option
where
F: FnOnce(T) -> U
{
match (self, f) {
(Some(value), Some(func)) => Some(func(value)),
_ => None,
}
}
}
fn pure<T>(value: T) -> Option<T> {
Some(value)
}
fn main() {
let a = Some(5);
let b = Some(3);
// now I could apply multi-argument functions
let result = pure(|x| |y| x + y)
.apply(a)
.apply(b);
println!("{:?}", result); // Some(8)
// or with a helper that felt more readable
fn lift2<A, B, C, F>(f: F, a: Option<A>, b: Option) -> Option<C>
where
F: FnOnce(A, B) -> C
{
match (a, b) {
(Some(x), Some(y)) => Some(f(x, y)),
_ => None,
}
}
let result2 = lift2(|x, y| x + y, Some(5), Some(3));
println!("{:?}", result2); // Some(8)
} An applicative functor adds two capabilities beyond regular functors:
- Pure/Return: A way to lift a value into the context
- Apply: A way to apply functions inside the context to values inside the context
This let me work with functions of any arity while keeping the “fail-fast” semantics of Option. If any input was None, the whole thing would be None.
The Big One: Dependent Computations Then I encountered the pattern that really made everything click. What if the computation itself could fail? fn safe_divide(a: i32, b: i32) -> Option<i32> {
if b == 0 { None } else { Some(a / b) }
}
fn safe_sqrt(x: i32) -> Option<f64> {
if x < 0 { None } else { Some((x as f64).sqrt()) }
}
fn main() {
let number = Some(16);
// I tried using map, but...
// let result = number.map(|x| safe_sqrt(x));
// this gave me Option<Option<f64>> -- not what I wanted!
// then I discovered and_then
let result = number.and_then(|x| safe_sqrt(x));
println!("{:?}", result); // Some(4.0)
// and I could chain computations that each might fail
let complex_result = Some(20)
.and_then(|x| safe_divide(x, 4)) // Some(5)
.and_then(|x| safe_divide(x, 0)) // None - stops here
.and_then(|x| safe_sqrt(x)); // never executed
println!("{:?}", complex_result); // None
} This was the monadic breakthrough. The .and_then() method (called flat_map or bind in other languages) automatically flattened the nested Options and short-circuited on the first None. I tried to formalize what I'd discovered: trait Monad<T> {
// lift a value into the monadic context fn return_value(value: T) -> Self; // bind/flat_map -- the core monadic operation fn bind<U, F>(self, f: F) -> Option where F: FnOnce(T) -> Option;
}
impl<T> Monad<T> for Option<T> {
fn return_value(value: T) -> Self {
Some(value)
}
fn bind<U, F>(self, f: F) -> Option
where
F: FnOnce(T) -> Option
{
match self {
Some(value) => f(value),
None => None,
}
}
}
fn main() {
let result = Option::return_value(16)
.bind(|x| safe_sqrt(x))
.bind(|x| if x > 3.0 { Some(x * 2.0) } else { None });
println!("{:?}", result); // Some(8.0)
} A monad is an endofunctor with two additional operations:
- Return/Pure: Lifts values into the monadic context
- Bind/FlatMap: Sequences computations that return monadic values
And it must satisfy three laws:
- Left identity: return(a)≫=f=f(a)
- Right identity: m≫=return=m
- Associativity: (m≫=f)≫=g=m≫=(λx.f(x)≫=g)
I tested these: fn main() {
// left identity: return(a).bind(f) == f(a)
let a = 5;
let f = |x| if x > 0 { Some(x * 2) } else { None };
let left = Option::return_value(a).bind(f);
let right = f(a);
println!("Left identity: {:?} == {:?}", left, right); // Some(10) == Some(10)
// right identity: m.bind(return) == m
let m = Some(42);
let left = m.bind(Option::return_value);
let right = m;
println!("Right identity: {:?} == {:?}", left, right); // Some(42) == Some(42)
// associativity was harder to test concisely,
// but it ensures the order of binding doesn't matter
} That’s when I understood. A monad isn’t some mystical concept — it’s just a pattern for chaining operations where each step might introduce effects (like failure, multiple values, asynchrony). The laws ensure that the chaining behaves predictably.
Suddenly Seeing Monads Everywhere Once I recognized the pattern, I started seeing it throughout Rust: Result<T, E> -- Handling Errors Monadically use std::num::ParseIntError;
fn parse_and_double(s: &str) -> Result<i32, ParseIntError> {
s.parse::<i32>() .map(|x| x * 2) // functor behavior
}
fn parse_divide_and_format(a: &str, b: &str) -> Result<String, String> {
// the ? operator is just bind/and_then in disguise!
let num_a: i32 = a.parse().map_err(|e| format!("Parse error: {}", e))?;
let num_b: i32 = b.parse().map_err(|e| format!("Parse error: {}", e))?;
if num_b == 0 {
return Err("Division by zero".to_string());
}
Ok(format!("{}", num_a / num_b))
} The ? operator is syntactic sugar for monadic bind. Every time I wrote value?, I was using a monad! Vec<T> -- The Non-determinism Monad fn main() {
let numbers = vec![1, 2, 3];
// functor behavior
let doubled: Vec<i32> = numbers.iter().map(|x| x * 2).collect();
println!("{:?}", doubled); // [2, 4, 6]
// monadic behavior -- flat_map represents "branching" computations
let expanded: Vec<i32> = numbers
.iter()
.flat_map(|&x| vec![x, x * 10])
.collect();
println!("{:?}", expanded); // [1, 10, 2, 20, 3, 30]
// each element "branches" into multiple possibilities
} Future<T> -- Asynchronous Computations use std::future::Future;
async fn fetch_user_id() -> Option<u32> {
// simulate async operation Some(42)
} async fn fetch_user_name(id: u32) -> Option<String> {
// simulate async operation
Some(format!("User{}", id))
} async fn get_user_info() -> Option<String> {
// monadic chaining in async context
// the ? operator works here too!
let id = fetch_user_id().await?;
let name = fetch_user_name(id).await?;
Some(format!("ID: {}, Name: {}", id, name))
}
How the Pieces Fit Together I started to see how each abstraction built on the previous one:
- Monoid: Combine values associatively with an identity element
- Functor: Transform values inside a context
- Applicative: Apply multi-argument functions in a context
- Monad: Sequence context-producing computations
The key insight: monads are endofunctors (they map from a category to itself) with extra structure. They provide ways to:
- Lift values into the monadic context (return/pure)
- Sequence computations that produce monadic values (bind/≫ =≫=/and_then)
Why This Matters Understanding these patterns made me a better Rust programmer than before:
- Error Handling: I now understood why the ? operator felt so natural -- it's monadic bind for Result<T, E>
- Null Safety: Option<T> operations became intuitive instead of mysterious
- Async Programming: Future combinators made sense
- Iterator Chains: I recognized functorial and monadic operations everywhere
- Parser Combinators: Libraries like nom clicked -- they're all about monadic composition
Coming Full Circle: Understanding Haskell After learning monads through Rust, I did something I hadn’t done in years — I opened up my Haskell book again and turned to the chapter I struggled. The type class definition that once seemed impenetrable suddenly made sense: class Monad m where
return :: a -> m a (>>=) :: m a -> (a -> m b) -> m b
I could now read this clearly:
- return is just Some() in Rust -- it lifts a value into the monad
- >>= (bind) is and_then() -- it chains computations that produce monadic values
- The type m a -> (a -> m b) -> m b says: "give me an m a and a function that turns a into m b, and I'll give you back m b"
That’s exactly what Rust’s and_then() does: impl<T> Option<T> {
fn and_then<U, F>(self, f: F) -> Option
where
F: FnOnce(T) -> Option // same shape as (a -> m b)!
{
match self {
Some(value) => f(value),
None => None,
}
}
} The monad laws, which once felt like arbitrary mathematical requirements, now made intuitive sense: Left identity: return a >>= f ≡ f a In Rust: Some(a).and_then(f) == f(a) Wrapping in Some then binding is the same as just calling f
Right identity: m >>= return ≡ m In Rust: m.and_then(Some) == m Binding with Some does nothing
Associativity: (m >>= f) >>= g ≡ m >>= (\x -> f x >>= g) In Rust: m.and_then(f).and_then(g) == m.and_then(|x| f(x).and_then(g)) The order of chaining doesn't matter The list monad example that confused me back then: instance Monad [] where
return x = [x] xs >>= f = concat (map f xs)
-- usage [1,2,3] >>= \x -> [x, -x] -- [1,-1,2,-2,3,-3] Now I could see it was identical to Rust’s flat_map: fn main() {
let numbers = vec![1, 2, 3];
let result: Vec<i32> = numbers
.into_iter()
.flat_map(|x| vec![x, -x])
.collect();
println!("{:?}", result); // [1, -1, 2, -2, 3, -3]
} Both represent non-deterministic computation — each element “branches” into multiple possibilities. The mysterious IO monad started making sense too. It wasn’t compiler magic — it was a way to sequence operations that have side effects: main :: IO () main = do
putStrLn "What's your name?"
name <- getLine -- bind: IO String -> (String -> IO ()) -> IO ()
putStrLn ("Hello, " ++ name)
This was doing the same thing as Rust’s ? operator with Result: fn main() -> Result<(), std::io::Error> {
use std::io::{self, Write};
print!("What's your name? ");
io::stdout().flush()?;
let mut name = String::new();
io::stdin().read_line(&mut name)?; // bind with ?
println!("Hello, {}", name.trim());
Ok(())
} Both use monads to sequence operations with effects (IO effects in Haskell, potential errors in Rust), and both short-circuit on failure. The do-notation that seemed like special syntax was just sugar for and_then chains: -- do-notation calculation :: Maybe Int calculation = do
x <- safeDivide 10 2 y <- safeDivide x 2 return (y + 1)
-- desugars to calculation' :: Maybe Int calculation' =
safeDivide 10 2 >>= \x -> safeDivide x 2 >>= \y -> return (y + 1)
In Rust, I’d write the same thing: fn calculation() -> Option<i32> {
safe_divide(10, 2) .and_then(|x| safe_divide(x, 2)) .map(|y| y + 1)
}
// or with ? operator (if we made a macro for Option) fn calculation_alt() -> Option<i32> {
let x = safe_divide(10, 2)?; let y = safe_divide(x, 2)?; Some(y + 1)
} The abstract Haskell code I struggled with a decade ago finally clicked because I’d built the intuition through Rust. I wasn’t learning definitions anymore — I was recognizing patterns I already knew, just dressed in different syntax. Looking back at my younger self struggling with Chapter 9, I realize the problem wasn’t that monads were too abstract. It was that I needed to discover the pattern in concrete code first, then appreciate the abstraction. Rust gave me that concrete foundation, and Haskell’s elegance finally made sense.
Lessons Learned Monads aren’t abstract mathematical curiosities — they’re patterns I was already using. By starting with Rust’s Option<T> and gradually extracting the underlying patterns, I learned:
- Monoids give us safe ways to combine values
- Functors let us transform values in context
- Applicatives handle multi-argument functions in context
- Monads sequence dependent computations
The next time I write .map().and_then().map() in Rust, I know I'm not just chaining method calls -- I'm using patterns that have proven themselves across decades of programming language design. The beauty of monads isn’t in their category theory origins. It’s in how they capture common programming patterns and make them reusable, predictable, and composable. In Rust, I get to use these powerful abstractions while keeping the performance and safety guarantees that make systems programming practical. I don’t think about monads every time I write code. But understanding them gave me a vocabulary for patterns I was already using and helped me recognize those same patterns in unfamiliar contexts. That’s been more valuable than any amount of category theory could have been.
Read the full article here: https://medium.com/@saehwanpark/how-i-learned-monads-not-through-haskell-but-through-rust-f4233f7779c7