Everyone’s Building AI Wrong — There’s Only One Kernel That Works

One AI Kernel to Rule Them All. Image created by the author with Stable Diffusion.

The Missing Piece That Keeps AI Subpar Think about what Unix gave us: the same kernel handles a single process doing computation, a server handling requests, a distributed system with thousands of concurrent processes. You don’t switch operating systems when you go from batch processing to interactive to networked. 😆

Now look at AI. We have completely different stacks for training (PyTorch), inference (ONNX, TensorRT), and agents (LangChain, AutoGPT). No shared invariants. No common type system. Each transition is a potential source of silent breakage. This is insane. The mathematical structure of a concept doesn’t change because you’re training versus inferring. The geometry of your embedding space is the same whether one model is querying it or twelve agents are.

We need an AI Orchestrator Stack — an AI Kernel — that unifies these modes, instead of three separate ecosystems held together with duct tape and prayer.

The Unified Vision

An AI-Kernel would make modes into

configurations, not architectures. Same geometric primitives. Same jet types. Same composition laws. APEL (Agent Process Execution Language) activates when you need orchestration. Checkpointing works whether you’re saving training state or agent workflow state.

Why Current Fragmentation Kills Us

Three boundaries. Three places to silently break everything: Training → Inference: You optimize for deployment and accidentally lobotomize the model. Inference → Agents: Black boxes calling black boxes. What could go wrong? Everything. Agents → Training: Fine-tuning on agent outputs without checking geometry. Congratulations, you’ve automated chaos.

The AI OS eliminates these boundaries. One mathematical foundation. One type system. One orchestration layer. Three modes that actually know about each other. The Mathematical Foundation: Why Linear Algebra Isn’t Enough

The Question Very Few Asks

Here’s the architectural puzzle everyone avoids: if all our computation ultimately reduces to matrix multiplication on GPUs — yep,pure linear algebra — how can we claim to handle curved, non-Euclidean spaces at all where the AI really lives? You can see it clearly in Figure 2: once you introduce the usual mechanisms of modern AI, your beautiful tangents, linear paths, local frames, commutativity, and geometric depth all become twisted, dragged off-axis, tilted, broken — distortions magnified at every layer.

And there it is: the linear algebra inside your favorite AI stack — PyTorch, JAX, TensorFlow, you name it — built a curved world it has no tools to navigate.

Of course the linear algebra is right locally, but wrong globally: because the AI landscape is a manifold: locally an euclidean flatland, globally a curved landscape (hyperbolic and toroidal for most cases).

This is answer that the differential geometry itself is giving to us, and it’s surprisingly hopeful: every curved surface is locally flat. That’s not a compromise — it’s a theorem.

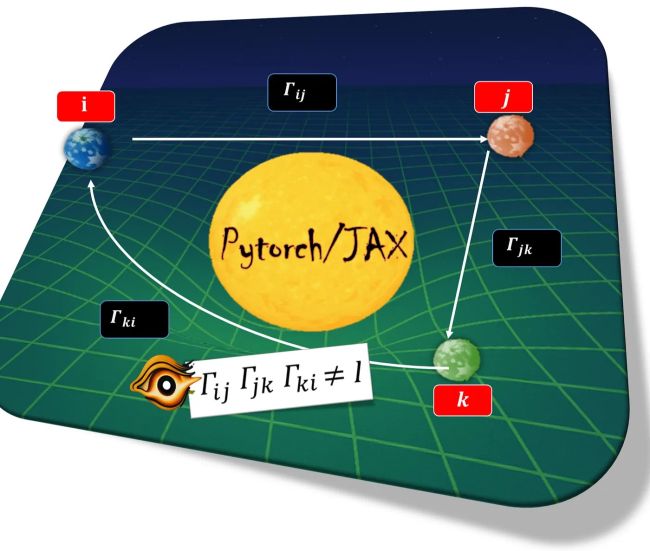
At any single point on a sphere, a torus, or a high-dimensional manifold, there exists a small neighborhood that looks exactly like ordinary flat space. The tangent plane at that point is a genuine vector space where linear algebra works perfectly. So linear algebra isn’t wrong. It’s incomplete. Still skeptical? Please read this one. The problems arise in three specific situations, all visually displayed in Figure 1 below.

Moving between points. The flat patch around point k is a different flat patch than the one around point j. They’re different vector spaces. You can’t just subtract vectors from different patches like they live in the same space: you need rules for translating between them. Mathematicians call this parallel transport. Going around loops. Just because every small patch is flat doesn’t mean the whole surface is flat. To see this visually, walk a triangle on Earth’s surface: you turn a total of only 270°, not the 360° a flat plane would require. The missing 90° is holonomy:curvature revealed only when you complete a loop.

Covering the whole space. A curved surface can’t be described by a single flat coordinate system. You need multiple overlapping patches (like the overlapping pages of an atlas covering Earth). Linear algebra works fine within each patch, but someone must ensure consistency between patches.

Figure 1 : The Curved AI Space That Linear Algebra Cannot Reach. Image created by the author with Blender.

The slogan: Linear algebra is correct locally. But theAI kernel should enforce correctness globally. As you can see in Figure 1 above. Current frameworks do linear algebra at each step and hope global structure takes care of itself. It doesn’t. That’s where hallucination and concept drift emerge: local computations are fine, but nobody tracks what happens when you compose them across the manifold.

The Five Showcases: What Goes Wrong When You Pretend a Curved World Is Flat Every major framework you touch today — PyTorch, JAX, TensorFlow, and beneath them cuBLAS and cuDNN — quietly makes the same bet: that all of AI can be reduced to matrix multiplications in a globally flat space.

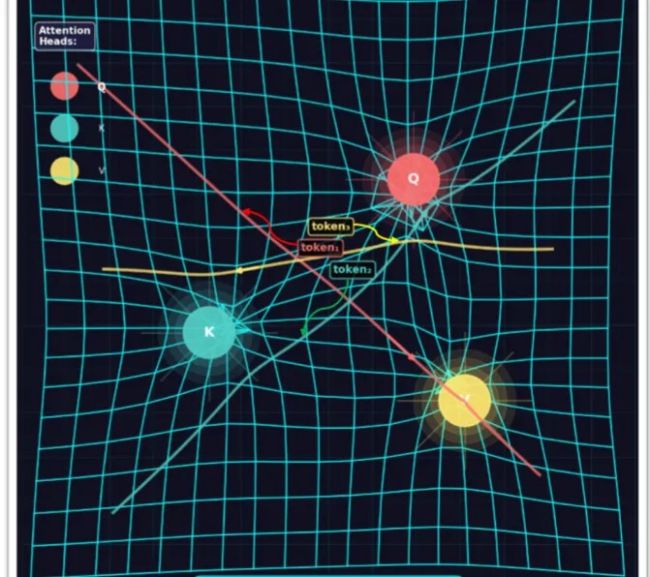
You saw this in Figure 1. Maybe you’re thinking: to make your AI landscape so curved, you need to pile on all those mechanisms — attention, embeddings, deep stacks of layers.

Now look at Figure 2 below, where we’ve added just the attention mechanism to a neural network. See what happens? The beautiful flat linear space created by your favorite AI stack becomes warped the moment attention heads start pulling on it. The grid lines that were straight and parallel now bend toward the attention heads like spacetime bending around massive objects. That’s not a metaphor: it’s what the math actually describes.

Figure 2. Attention bends the space between tokens.Image created by the author with Blender.

This is exactly what happens when you rely exclusively on linear algebra while ignoring the geometry underneath. It bears repeating: our AI tools — PyTorch, JAX, TensorFlow, and under all of them cuBLAS and cuDNN — reduce everything to matrix multiplications on GPU cores, silently assuming the space is flat everywhere. It isn’t.

And the consequences show up in failures we’ve normalized as “just how AI behaves.” Below are the most important showcases of this mismatch.

1. Hallucination as Accumulated Drift Your LLM invents a court case. It kills off a famous person prematurely. It fabricates scientific citations. And worse: it gives you catastrophic business advice with serious legal consequences. We shrug and say: It’s just predicting the next token. But why does the prediction drift into fiction? Each attention hop moves a representation across embedding space. If that space were flat, you could chain hundreds of hops and stay grounded. But the embedding manifold is curved. Each hop adds a tiny rotation: untracked, unbounded. After enough layers and enough reasoning steps, the representation has drifted so far that the model lands on something geometrically disconnected from truth. This isn’t randomness.  It’s curvature-driven drift that nobody measures.

2. The “Reversal Curse” in Language Models Research found a striking failure: Train a model on “A is B.” It fails to learn “B is A.”

Example: Tell it “Tom Cruise’s mother is Mary Lee Pfeiffer.” It learns that. Ask, “Who is Mary Lee Pfeiffer’s son?” — it often fails. Why? The standard explanation points to autoregressive training: the model learns to predict in one direction only. But there’s a deeper geometric reading:

In flat Euclidean space, relationships are symmetric: The vector from A→B is just the negative of B→A. But in a curved manifold, paths are direction-dependent. Parallel transport depends on the route you take. The path from A to B is not the same as the path from B to A. The model learned the forward path. The reverse path is different — and was never trained. Linear algebra says: “Just flip the arrow.” Geometry says: “There is no single arrow.” And the AI stack has no mechanism to learn both paths.

3. Long-Context Degradation Ask a model about page 3 of a long document → great answer. Ask about page 87 → worse. Ask about a link between page 12 and page 73 → confused. We’re told: Attention has limits. Context windows are hard. The geometric explanation goes deeper: Every token has to attend to others through curved embedding space. When token 50 “talks” to token 5000, the meaning of token 50 is transported through thousands of curved patches. Without tracked parallel transport, the meaning arrives rotated.

The model doesn’t know it’s rotated. It just continues doing linear algebra on distorted representations. Long context isn’t just hard because of compute or attention limits. It’s hard because curvature accumulates with distance.

4. Adversarial Fragility Change one pixel. The model flips from “panda” to “gibbon” with 99% confidence. The usual explanation: Adversarial examples exploit high-dimensional geometry. True… but incomplete. Which geometry? The frameworks assume Euclidean. The representation manifold isn’t.

The decision boundary is a hypersurface in a curved manifold. Near that boundary, tiny Euclidean changes can move you along curved geodesics. One pixel doesn’t change much in pixel space, but it can move the representation a huge distance on the manifold, crossing the boundary entirely. If frameworks tracked curvature, they could notice: This tiny input change produced a massive manifold displacement, flag it. But they don’t. They assume: small input change → small effect. Which is exactly wrong when the AI is living in a curved space.

5. Concept Drift in Fine-Tuning You fine-tune a model on a company’s documents. At first, it works great. Then, gradually, it starts hallucinating, mixing your terminology with invented facts, forgetting things it used to know.

We explain this with “catastrophic forgetting” or “distribution shift.”

Geometrically, something else is happening: Fine-tuning moves the model’s parameters along a path in a curved space. Your updates looked good locally: the loss decreased. But globally, you’ve wandered into a region of parameter space where old knowledge is no longer reachable. Not destroyed…just separated by curvature.

Recent research on model merging confirms this: separately trained models can often be reconnected by finding the right path through parameter space. The knowledge was never erased: it became geometrically inaccessible. Linear algebra optimized the local patch. Nobody checked where you ended up globally.

The Unifying Diagnosis These are not five separate issues. They are the same geometric failure expressed in five different ways: Local linear operations performed on a globally curved manifold, without tracking the accumulated geometric cost.

Until AI systems account for curvature — and until we have a kernel that tracks transport, measures distortion, and prevents drift — these failures will keep reappearing, no matter how big the models get. The diagnosis is clear. Now lets go for the prescription.

The Five Rescuing Components of the AI Kernel

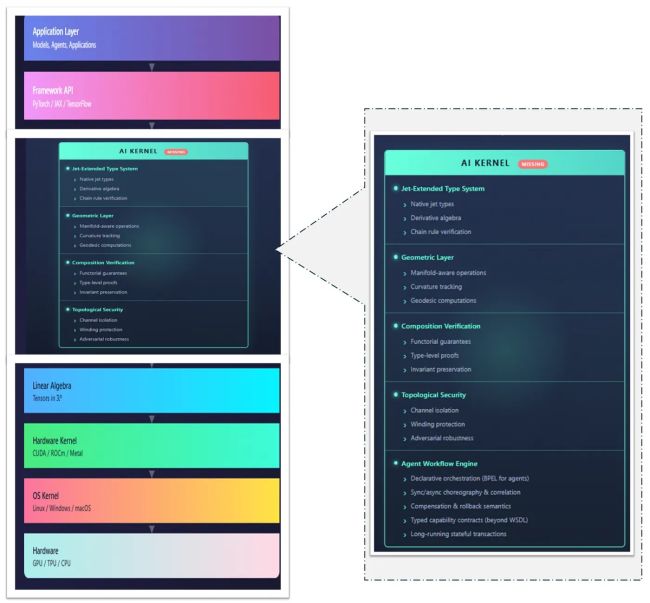
Just as a traditional OS kernel provides memory management, process isolation, file systems, and security — the AI Kernel provides five analogous services for intelligent computation (see Figure 3 below). Crucially, the same five components serve all three modes: training, inference, and multi-agent orchestration.

Figure 3. Your app sits on PyTorch. PyTorch sits on CUDA. CUDA sits on Linux. Linux sits on hardware. Every layer has a kernel providing guarantees: memory protection, process isolation, resource management. Now look at the zoomed box: that’s what should sit between your framework and the raw linear algebra. Jet types for derivative verification. Geometric awareness for non-Euclidean embeddings. Composition laws that actually compose. Agent orchestration that doesn’t devolve into infinite loops. It’s not radical, just the obvious layer nobody’s building. Figure created by the author using Manim

1. Jet-Extended Type System The problem: Current autodiff systems compute derivatives but discard the algebraic relationships between them.  When you chain layers, the chain rule applies. Yep…but nothing verifies it was applied correctly. Your gradients could be lying to you. They probably are.

The mathematics:  A k-jet at point x is the equivalence class of all functions sharing derivatives up to order k. Jets form an algebra with well-defined composition rules. Value plus all derivatives up to order k becomes a first-class mathematical object — a structured type the kernel can verify. Across modes:

During training, jet types catch vanishing gradients before instability hits.
During inference, they verify that output sensitivities match expected behavior.
In multi-agent systems, they ensure tool calls preserve derivative structure when agents chain computations.

2. Geometric Layer The problem: Everything in current deep learning lives in flat Euclidean space ℝⁿ. But:

Hierarchies are inherently hyperbolic.
Periodic patterns are inherently toroidal.
Probability distributions are inherently curved.

Forcing all of this into flat space is like insisting the Earth is flat because your map is flat. It works… until you try to sail to India and hit the Americas.🤔 Want the evidence?  Poincaré embeddings ( read this paper) showed that hyperbolic space embeds tree structures with exponentially less distortion than Euclidean space. A tree with n nodes needs O(n) dimensions in ℝⁿ, but only O(log n) in hyperbolic space. This isn’t armchair theory: it’s measured on real datasets.

Across modes:

During training, the geometric layer ensures learned embeddings respect the manifold structure.
During inference, holonomy checks verify that concept traversal remains coherent.
For agents, shared geometric context means Agent B understands concepts in the same curved space as Agent A.

3. Composition Verification The problem: Neural network layers compose by stacking. Dimensions match syntactically, but nothing verifies semantic correctness.

Does fine-tuning preserve safety properties?
Does merging LoRA adapters produce consistent behavior?

Currently: deploy and pray. The official term is “empirical validation.” Same thing 👀

The category-theoretic perspective: Layers are morphisms between typed tensor spaces. Composition should preserve declared properties. Lipschitz bounds, equivariance, monotonicity: the kernel checks that these survive composition instead of vanishing quietly in a pull request. In plain english: Think of it like contract law for neural networks. Each layer signs a contract:

I promise to be smooth I promise to be fair to rotations I promise not to flip signs randomly.

When you merge two layers, do the contracts still hold? Right now, you find out in production… ouch, late on a Saturday night.

Across modes:

Training: verifies that optimization preserves architectural invariants.
Inference: verifies that quantization or pruning maintains declared properties.
Multi-agent: verifies that chaining agent outputs respects type contracts.

4. Topological Security

The problem: In current architectures, any input can potentially affect any output. There is no mathematical isolation. This is why adversarial examples work: small input perturbations cause large output changes because there’s no structural barrier.

The speculative idea: In physics, topologically protected states derive robustness from global invariants that can’t be changed by local perturbations. Think of a knot in a rope: you can’t untie it by wiggling one spot; you need global access.

Could architectures with toroidal or non-trivial topology provide analogous protection? Could winding numbers create guaranteed separation between processing channels? We have some good empirical and mathematical reasons to think so.

Honest caveat: And yet, this is the most speculative component. If the other four are engineering, this one is still physics envy. But the principle: robustness from global structure rather than local tuning, deserves exploration across all modes.

5. APEL: Agent Process Execution Language The problem: Single AI models already hallucinate and forget context. Now we’re putting these chaotic systems in charge of orchestrating other chaotic systems.

Agent A calls Agent B
Agent B spawns Agents C and D
Errors compound
Context fragments

Production systems end up with infinite delegation loops, orphaned processes, cascade failures, and debugging sessions that feel like exorcisms. The precedent: We solved this in 2003 with BPEL for web services:

Declarative workflows
Compensation handlers
Correlation sets
Typed contracts
Long-running transaction management

Then microservices happened, REST won, and everyone forgot orchestration was a solved problem. History doesn’t repeat, but it does rhyme… badly. APEL provides:

Declarative workflow definitions
Compensation semantics (if step 5 fails, automatically undo steps 1–4)
Correlation and context threading
Typed agent contracts with enforced constraints
Deadlock and loop detection
Checkpoint and resume for long-running workflows
Full observability with execution traces

Across modes: APEL activates primarily for multi-agent orchestration — but:

The same checkpointing works for training state.
The same observability traces model behavior during inference.

The kernel doesn’t have “agent mode” — it has orchestration primitives that scale from one process to thousands.

And here you go: five components. One kernel.  One kernel to rule them all, one kernel to guard them, one kernel to bind them against chaos. 😁

The same architecture that catches vanishing gradients during training also flags adversarial inputs during inference and prevents delegation loops during orchestration.

Geometry doesn’t care what mode you’re in. Neither does Murphy’s Law.

Why This Matters: From Artisanal to Industrial AI

Right now AI engineering is artisanal. Prompt tweaking, hyperparameter tuning. it works on my dataset.  No principled debugging. No formal guarantees. The “AI engineer” of 2024 calls model.fit() and… right, prays.

The AI-Kernel gives a path to industrial AI: repeatable, verifiable, maintainable. The same transition that happened from assembly hacking to structured programming to operating systems.

The AI engineer of the future isn’t someone who calls model.fit(). It’s someone who understands:

• What geometric space their concepts live in • How composition affects invariants • Where global coherence can break despite local correctness • How to orchestrate agents with compensation and rollback

The Path Forward

The good news: the math and distributed-systems theory already exist. Jets are from the 1950s . Geometric deep learning is active research. BPEL solved orchestration in 2003. The building blocks are documented.

They’re just sitting in different rooms, not talking to each other. The missing piece isn’t more research: it’s integration. One coherent kernel that serves training, inference, and multi-agent orchestration with the same mathematical foundation. This isn’t speculation about what AI might need someday. This is technical debt we’re accumulating with every deployment. The question isn’t whether the industry arrives at this architecture: it’s whether it takes 3 years or 10. One kernel. Three modes. Zero excuses.

The architects who understand the missing kernel — mathematical, geometric, orchestration-level — will define the next era of AI. The rest will keep wondering why their models drift, forget, and hallucinate.

Which side are you building for?

Read the full article here: https://ai.gopubby.com/the-one-ai-kernel-you-need-to-rule-everything-else-2b0685ff657f