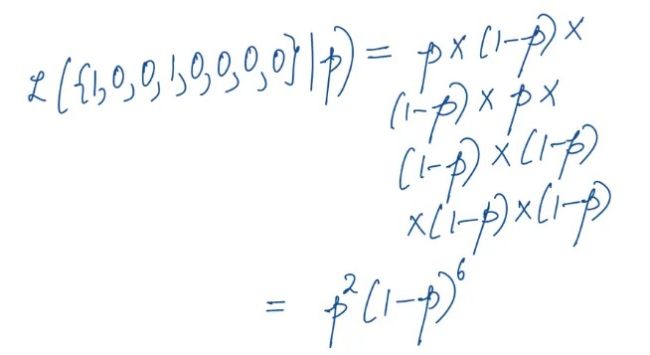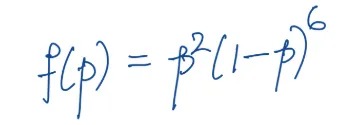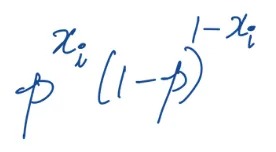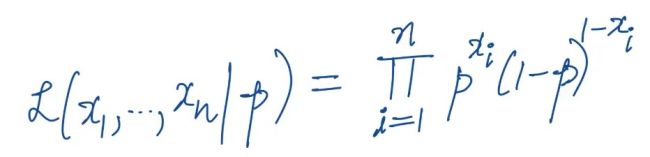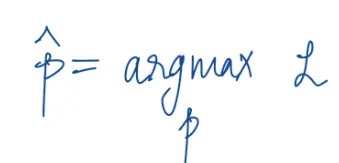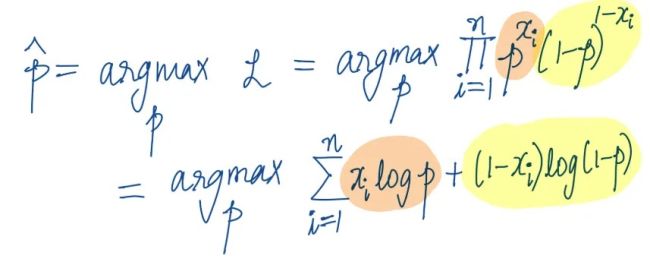This embarrassingly simple secret explains all of AI
Credits: Leonardo AI In college, there was a course called “PRML”, the infamous ML elective that pretty much everyone wanted to take. When I first heard about it, my seniors told me to take probability first. But why was probability important for ML? I had no idea.
If you like learning AI concepts through easy-to-understand diagrams, I’ve created a free resource that organises all my work in one place — feel free to check it out! Your free one-stop guide to AI in 2025 The only guide you'll ever need to master AI and LLMs. nikhilanand03.substack.com
When I finally learnt probability, I realised something most ML textbooks don’t spell out:
Every single AI model can be seen as a probability problem.
When I realised that, the field became so much more intuitive. In this blog, you’ll learn something I wish I knew when I first started: Probability is literally the foundation that the whole field of AI stands on.
Meet Mario (and his mystery machines)
First, let’s say “Hi” to Mario.
Suppose Mario encounters a strange machine in the Mushroom Kingdom. Every time he presses a button, the machine spits out either a Goomba or a One-Up mushroom.
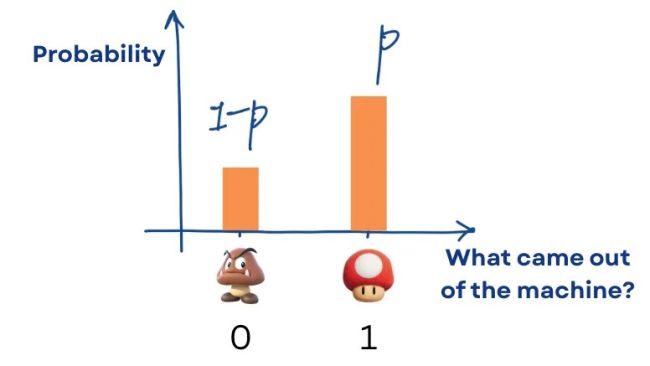
A machine spits out either a goomba or a 1-up mushroom every time you press the button. (Image by author)
Let’s say the machine has some internal parameter p that represents the probability of getting a 1-up. For instance, if p = 0.5, the machine flips a fair coin, heads gives a 1-up, tails gives a Goomba.
Now to keep it simple, let’s represent the goomba with the number 0, and the 1-up with the number 1.
Here’s how the probability distribution looks for the machine.
Now if Mario has a lot of machines, he wants to be able to pick the machine with the highest probability of outputting a 1-up.
But he needs to know p for that, which he doesn’t. How does he figure out what p is?
The challenge: estimating p
Mario decides to run an experiment. For one machine, he presses the button 8 times and gets these outputs:
{1,0,0,1,0,0,0,0,}
What do you think p is? Mario’s intuition says 1/4. He got 2 1-ups in 8 tries, which means roughly 1 1-up every 4 tries.
But Mario wanted to be rigorous. In his tough world, there was no room for error.
Why intuition alone isn’t enough Here’s the thing: p could still be anything.
For instance, let’s say p=0.5. That means both 1 and 0 are equally likely.
Even at p = 0.5, it’s still possible to get that exact sequence {1, 0, 0, 1, 0, 0, 0, 0}. At every turn, the probability of that number being outputted is 0.5.
At every push of the red button, the probability of either 1 or 0 coming out is 0.5. (Image by author) So if we multiply 0.5 by itself 8 times, we get the total probability of that exact sequence. ) Introducing the likelihood function At this point, what we know is that we got a sequence {1, 0, 0, 1, 0, 0, 0, 0} from the machine. If we assume the parameter of p, what is the likelihood that we would get this sequence?
At every push of the red button:
- To get a 1, there’s a probability of p.
- To get a 0, there’s a probability of (1-p).
The likelihood of observing this sequence, given some value of p, is:
L(A|B) reads as “likelihood of getting sequence A given that the parameter is p”. (Image by author) L( {1,0,0…} | p ) reads as, the “likelihood of a sequence {1,0,0…} given a parameter of p. This is called the likelihood function. It tells us: for a given value of p, how likely were we to observe this data?
Maximum likelihood estimator
One of several ways to estimate p is to simply find the value of p at which the likelihood is maximised. Aptly called the “maximum likelihood estimator”. And to find the value of p, we ask this question: At what value of p is this likelihood maximised? At this point, the likelihood function looks like this:
Mario plotted this function to visualise it.
For any value of p, the y-axis tells us the likelihood of getting the sequence that we got. (Image by author) The peak occurs at p = 0.25.
Wait. Mario was right earlier! His intuition of 1/4 was correct. But is it always this simple? The general case Let’s say we get a sequence of n outputs: {x₁, x₂, x₃, …, xₙ}, where each xᵢ is either 0 or 1.
What’s the likelihood of this sequence? Well, for any xᵢ = 0, the probability is (1-p). For xᵢ = 1, the probability is p.
We can write this compactly as:
If you’re wondering how we got to this compact expression, think about it: For any 0 in any sequence, we’d set x_i to 0 and the expression would become (1-p). And for any x_i=1, the expression would be p.
To get the likelihood of the entire sequence, we multiply these probabilities across all data points:
Pi represents a product, which simply is equivalent to multiplying those terms (p or 1-p) across the n different datapoints. (Image by author) Now we have a function that depends on both p and our observed data points xᵢ. The optimisation problem We want to find the p that maximises this likelihood. We can write this as an optimisation problem:
The optimal parameter p is the one that maximises the likelihood function. (Image by author) Here’s a trick: since the logarithm is a monotonically increasing function, maximising L(p) is the same as maximising log(L(p)).
Taking the log:
Do you recognise this? This is the categorical cross-entropy loss function that neural networks use during training. It looks complicated, but now you know that it stems from the most simple idea: maximise the likelihood of seeing the data.
Solving for p
Anyway, to optimise any function, we take the derivative and set it to zero. If you’re unfamiliar with derivatives, check this out:
Understanding derivatives from a falling apple Apples, derivatives and AI have more in common than you think. open.substack.com
Setting it to zero and simplifying, we get:
And simplifying some more:
In other words, p equals the average of all the xᵢ values.
That’s pretty intuitive
The maximum likelihood estimate is just the average! For example, if Mario gets the sequence {0, 1, 0, 0, 0, 1, 0, 1, 0}, the most likely p value is 3/9 = 0.33, since there are three 1s and six 0s. Or if he gets {1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 0}, the estimate is 7/13 ≈ 0.54. Simple.
Why does this matter in AI?
So far, the model we looked at just estimated a distribution in general. It’s unsupervised.
There’s no “input” to the model, just an output when you press a button. But what if the machine Mario was using was an LLM?
LLMs are input-conditioned machines
An LLM is an “input-conditioned machine”. Mario needs to first pass a sentence as input before getting the output.
The distribution is now conditioned on the input. So when I ask “Who is POTUS?” I get one distribution, but when I ask “Who is the CEO of Apple?” I get anohter.
The act of training the LLM is essentially the same as estimating this distribution (which is equivalent to finding the value of p like we did earlier). Let me explain why.
Training an LLM = estimating a distribution
When you ask “Who is POTUS?” to an LLM, it internally frames a distribution f(xᵢ | “Who is POTUS?”). Let’s say during training, the LLM has seen several paragraphs like this.
It has seen Trump as a continuation of that specific phrase twice and it has seen Obama as a continuation once.
So similar to pressing the button on the machine, we get a list of all the possible answers the LLM has seen before:
{“obama”,”Trump”,”Trump”,…}
When we’re training the LLM, it estimates its distribution simply based off of what it has seen before. Using the same MLE approach, the model estimates:
- p(Trump | “Who is POTUS?”) = 2/3 = 0.66
- p(Obama | “Who is POTUS?”) = 1/3 = 0.33
Probability of “obama” is 1/3 and probability of “trump” is 2/3. (Image by author) When you think of LLM training this way, it’s a lot easier to see why it works, instead of looking at it from the perspective of some abstract “categorical cross-entropy minimisation”.
The big picture
When you interact with ChatGPT or Claude, you’re essentially querying a massive probability distribution. The model has seen billions of text sequences during training. For each possible input, it’s estimated the distribution of next tokens that maximises the likelihood of all that training data. That’s Maximum Likelihood Estimation at scale.
If you like learning AI concepts through easy-to-understand diagrams, I’ve created a free resource that organises all my work in one place — feel free to check it out!
Your free one-stop guide to AI in 2025 The only guide you'll ever need to master AI and LLMs. open.substack.com=
Conclusion
In this blog, we covered how probability and Maximum Likelihood Estimation form the foundation of how language models learn.
We started with Mario and his mystery machines to build intuition for the problem. Then we formalised it mathematically, showing that the MLE estimate is simply the average of observed outcomes. Finally, we connected this to LLMs, showing that categorical cross-entropy, the loss function used in training, is just MLE in disguise.
The key insight? When an LLM predicts the next word, it’s not doing anything magical. It’s estimating probability distributions that best explain the training data it’s seen. This same principle, maximising likelihood, underlies nearly every machine learning model, from simple classifiers to GPT-4.
Read the full article here: https://ai.gopubby.com/stop-learning-ai-backwards-e20bd7d7d2cb